Space Complexity

It can be defined as:

Order of growth of memory space in terms of input size.

Let’s consider some examples:

    def sum(n):
        return n * (n + 1)//2

The space complexity is $\Theta(1)$ since only 1 variable is needed.

def sum2(n):
    sum = 0
    for i in range(1, n+1):
        sum += i
    return sum

The space complexity is still $\Theta(1)$ since only 3 variables are needed.

def arrSum(arr):
    sum = 0
    for i in arr:
        sum += i
    return sum

The space complexity is $\Theta(n)$ since we need array of size $n$ .

Auxiliary Space

Order of growth of extra space (any space other than needed for input and output) in terms of input size.

For the earlier arrSum example, aux space is $\Theta(1)$ and space complexity is $\Theta(n)$ .

For arrays and lists, the space complexity is anyways going to be $\Theta(n)$ .

Therefore, auxiliary space is an important criteria in analysis.

Consider the following function:

def recSum(n):
    if n <= 0:
        return 0
    return n + recSum(n - 1)

The function call stack for the invocation recSum(5) can be visualized as follows:

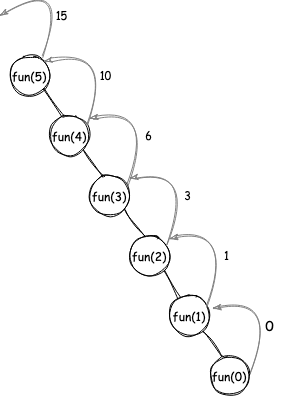
The number of stack frames is $n + 1$ .

The space complexity: $\Theta(n)$ .

Aux space: $\Theta(n)$ .

Consider the following fibonacci implementation:

def fib(n):
    if n == 0 or n == 1:
        return n
    return fib(n - 1) + fib(n - 2)

Expected results for values of $n$ :

Here is how the recursion tree will look like for fib(4) execution:

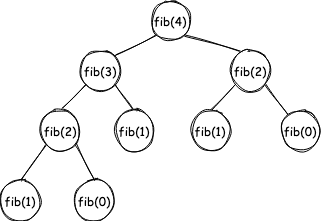
Let’s see how the call stack looks like for fib(4) execution:

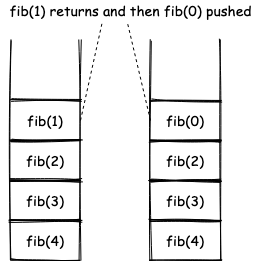
As we can see, the maximum number of active stack frames is $4$ i.e. height of tree.

Therefore aux space = $\Theta(n)$ .

The simple rule to find out the aux space for recursion: it’s always equal to the height of the recursion tree.

Consider the following non-recursive implementation for fibonacci:

def fib2(n):
    f = [None for _ in range(n)]
    f[0], f[1] = 0, 1
    for i in range(2, n):
        f[i] = f[i-1] + f[i-2]
    return f[n-1]

Space complexity: $\Theta(n)$ .

Aux space: $\Theta(n)$ .

Can we reduce the aux space needed?

Conside the following implementation:

def fib3(n):
    if n == 0 or n == 1:
        return n
    a, b, c = 0, 1, 0
    for i in range(2, n + 1):
        c = a + b
        a, b = b, c
        print(f"i={i}; c={c}, a={a}, b={b}")
    return c

Here is variable tracing looks like for above implementation for $n = 4$ :

a=0, b=1, c=0
i=2; c=1, a=1, b=1
i=3; c=2, a=1, b=2
i=4; c=3, a=2, b=3

Space complexity: $\Theta(1)$ .

Aux space : $\Theta(1)$ .